들어가며
새로운 공부를 하고 있는데, 내 주장을 펼치려면 사실에 근거한 자료로 뒷받침을 해주어야 한다. 논문을 작성하기 위한 연구방법론 중 하나를 소개한다. 사례 설명은 정보보안 분야와 접목해 보았다.
1. Fleiss' kappa 개요
Fleiss’ kappa(플라이스 카파)는 “여러 평가자(3명 이상)가 같은 대상들을 범주형(예: 취약/비취약, High/Med/Low)으로 판단했을 때, 그 판단 일치도가 우연 수준을 얼마나 ‘넘어서는지’를 수치로 보여주는 통계이다.
한 줄로 요약하면 “다수 평가자의 분류가 서로 얼마나 신뢰할 만하게 일치하는가?”이다.
2. 왜 필요한가?
정보보안 사례를 예를 들면 다음 같은 상황이 있을 수 있다.
- 여러 진단자가 같은 로그/취약점/이벤트를 보고
“이건 XSS다 / 아니다”, “심각도는 High/Med/Low다” 같은 범주로 라벨링함. - 혹은 자동화 도구가 만든 결과를 사람 여러 명이 다시 분류/검증함.
이때 단순히 “80% 일치했다”는 숫자는 애매합니다.
우연히도 80%가 맞을 수 있기 때문이다.
Fleiss’ kappa는
- 실제 일치율 P̄ 과
- 범주 분포만으로 기대되는 우연 일치율 P̄ e를 비교해서
“우연을 제거한 순수한 합의 수준”을 계산한다.
3. 언제 쓰는가?
평가자가 3명 이상인 경우에 사용한다. (두명일 경우에는 Cohen's kappa를 사용한다.) 대상(아이템)이 여러 개 있고, 각 아이템을 동일한 수의 평가자가 평가할 때 사용한다.
결과가 명목형/범주형(순서가 없는 라벨)
예: 취약/비취약, 공격유형(A,B,C), 탐지성공/실패
4. 계산 개념
(1) 데이터 형태
아이템 N개, 범주 k개, 평가자 n 명각 아이템마다 "범주별로 몇 명이 그 범주를 골랐는지"를 세어 표로 만든다.
(2) 아이템별 일치도 Pi
한 아이템 안에서 평가자들이 얼마나 모였는지. 같은 범주를 고른 쌍(pair)이 얼마나 되는지 세는 식이다.
모든 같은 범주를 선택했을 때 Pi=1 이된다.

(3) 전체 평균 일치도 P̄

(4) 범주별 선택 비율 p_j
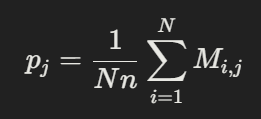
(5) 우연 일치 기대값 P̄ e

(6) Fleiss' kappa

분자: 실제 일치 - 우연 일치
분모: 가능한 최대(우연을 뺀) 일치
k=1 이면, 완전 일치
k=0 이면, 우연 수준
k<0 이면, 우연보다도 못한 합의(체계적 불일치)
5. 해석 기준(관행)
절대적인 법칙은 아니지만, 보통 수치별 해석은 다음과 같다.
< 0 : 합의가 우연보다 낮음
0.00~0.20 : Slight(아주 약함)
0.21~0.40 : Fair(약함)
0.41~0.60 : Moderate(보통)
0.61~0.80 : Substantial (강함)
0.81~1: Almost perfect(매우 강함)
'Report > Term paper' 카테고리의 다른 글
| [악성앱 분석 보고서] 안드로이드 피싱앱 행위 분석 (초대코드 입력앱 2) (0) | 2024.11.22 |
|---|---|
| 비타민과 미네랄 (0) | 2021.05.14 |
| [정보보안] 침투 테스트(Penetration Testing) 개요 (0) | 2021.03.08 |
| [컨텐츠 보안] Steganography 스테가노그래피 기법 (0) | 2020.12.16 |
| BUFFRER OVERFLOWS ON REDHAT 6.2 (0) | 2020.11.25 |

